Errors in Measurement and Significant Figures

The number of significant figures for the three number $161\mathrm{cm}, 0.161\mathrm{cm}, 0.0161\mathrm{cm}$  are:

The density of a cube is measured by measuring its mass and length of its sides. If the maximum error in the measurement of mass and length are $4\%$ and $3\%$ respectively, the maximum error in the measurement of density will be

The percentage errors in the measurement of mass and speed are  $2\%$ and  $3\%$  respectively. The error in kinetic energy obtained by measuring mass and speed will be:

In a vernier calliper $N$ divisions of vernier scale coincides with$(N-1)$  divisions of the main scale (in which length of one division is $1 \mathrm{mm}$). The least count of the instrument should be (in $\mathrm{cm}$):

A certain body weighs 22.42 gm and has a measured volume of 4.7 cc. The possible error in the measurement of mass and volume are 0.01 gm and 0.1 cc. Then maximum error in the density will be

A certain body weigh 22.42 gm and has a measured volume of 4.7 cc. The possible error in the measurement of mass and volume are 0.01 gm and 0.1 cc. Then maximum error in the density will be

Assertion : When percentage errors in the measurement of mass and velocity are $1\%$ and $2\%$ respectively, the percentage error in K.E. is $5\%$.

Reason :  $\frac{\Delta E}{E}=\frac{\Delta m}{m}+\frac{\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}2\Delta v}{v}$

Assertion: When percentage errors in the measurement of mass and velocity are $1\%$ and $2\%$, respectively, the percentage error in Kinetic Energy is $5\%$. 

Reason:  $\frac{\Delta E}{E}=\frac{\Delta m}{m}+\frac{\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}2\Delta v}{v}$ (where $E$ is the kinetic energy, $m$ is the mass and $v$ is the velocity). 

A student performs an experiment to determine the Young’s modulus of a wire, exactly $2 \mathrm{m}$ long, by Searle’s method. In a particular reading, the student measures the extension in the length of the wire to be $0.8 \mathrm{mm}$ with an uncertainty of $\pm 0.05 \mathrm{mm}$ at a load of exactly $1.0 \mathrm{kg}$. The student also measures the diameter of the wire to be $0.4 \mathrm{mm}$ with an uncertainty of $\pm 0.01 \mathrm{mm}$. Take $g=9.8 \mathrm{m} {\mathrm{s}}^{-2}$ (exact). The Young’s modulus obtained from the reading is

A student performs an experiment for determination of $g\left(=\frac{4{\pi }^{2}l}{T^2}\right)$. The error in length $l$ is $\mathrm{\Delta }l$ and in time $T$ is $\mathrm{\Delta }T$ and $n$ is number of times the reading is taken. The measurement of $g$ is most accurate for

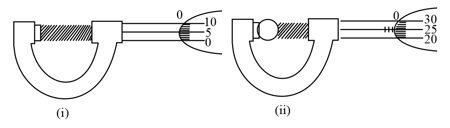
In a screw gauge, the zero of main scale coincides with fifth division of circular scale in figure (i). The circular divisions of screw gauge are $50.$ It moves $0.5 \mathrm{mm}$ on main scale in one rotation. The diameter of the ball in figure (ii) is:

The side of a cube is measured by vernier callipers ($10$ divisions of a vernier scale coincide with $9$ divisions of main scale, where $1$ division of main scale is $1 \mathrm{mm}$ ). The main scale reads $10 \mathrm{mm}$ and first division of vernier scale coincides with the main scale. Mass of the cube is $2.736 \mathrm{g}$. Find the density of the cube in appropriate significant figures.

The side of a cube is measured by vernier calipers ($10$ divisions of a vernier scale coincide with $9$ divisions of main scale, where $1$ division of main scale is $1 \mathrm{mm}$). The main scale reads $10 \mathrm{mm}$ and first division of vernier scale coincides with the main scale. Mass of the cube is $2.736 g$. Find the density of the cube in appropriate significant figures.

In Searle’s experiment, which is used to find Young’s Modulus of elasticity, the diameter of experimental wire is $D=0.05cm$ (measured by a scale of least count  $0.001cm$ ) and length is  $L=110cm$  (measured by a scale of least count $0.1cm$ ). A weight of 50 N causes an extension of  $X=0.125cm$  (measured by a micrometer of least count $0.001cm$ ). Find maximum possible error in the values of Young’s modulus. Screw gauge and meter scale are free from error.

If $n^{th}$ division of main scale coincides with $(n+1{)}^{th}$ divisions of vernier scale. Given one main scale division is equal to $\text{'}a\text{'}$ units. Find the least count of the vernier.

Two objects $A$and $B$are of length$5 \mathrm{cm}$ and $7 \mathrm{cm}$ are determined with errors$0.1 \mathrm{cm}$ and $0.2 \mathrm{cm}$ respectively. Error in their total length and difference of their lengths are

What is the number of significant figures $(3.20 +4.80) \times {10}^5$